Mastering Curve Fitting. How to Fit Complex Data with Parametric Splines
Fitting curves to data points is a crucial part of data analysis across many fields. Whether you need to model experimental measurements, approximate results of numerical analysis, extrapolate missing data, or just visualize relationships in your data – finding the right curve is essential for obtaining correct insights, predictions and estimates. Here we'll explore the basics of curve fitting, get an overview of the most common and universal methods, and learn how to easily find the best fit for your data using a free interactive curve fitting online tool integrated into SplineCloud.
What is Curve Fitting?
Curve fitting is the process of finding a mathematical function that closely matches a set of data points. The goal is to find a curve (or function) that models the relationship in the data as accurately as possible.
Some common use cases for curve fitting include:
- visualizing trends and patterns in data;
- predicting or extrapolating values;
- smoothing out noise and outliers;
- interpolating between known data points;
- understanding correlations between variables.
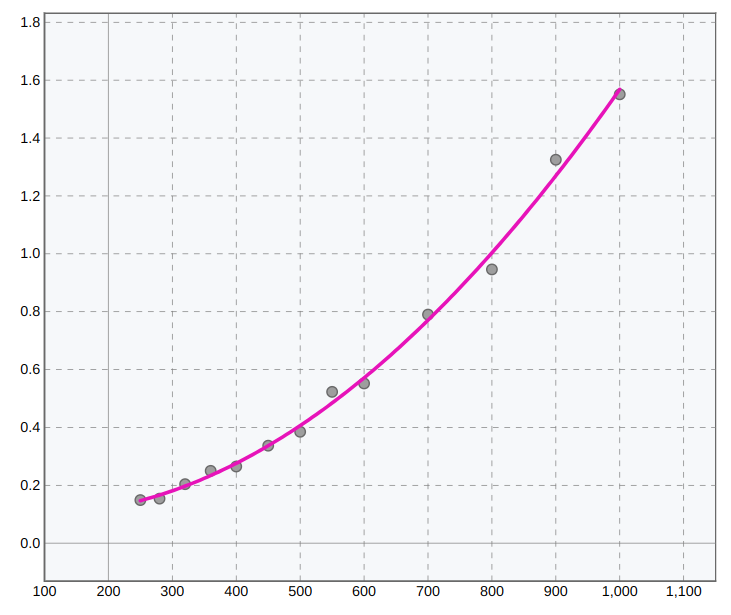
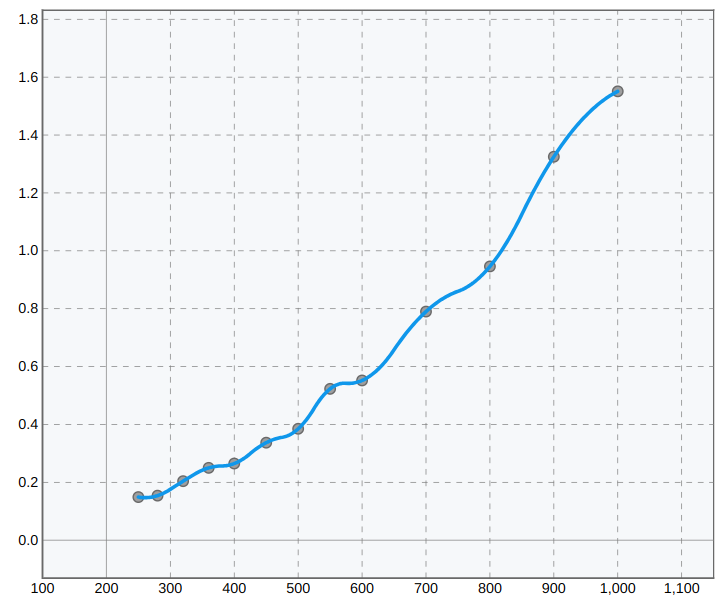
Fitting curve falls into two main categories: approximation (optimal fit) and interpolation (exact fit). The goal of approximation is to find a function that closely resembles the relationship represented by a set of data points. Interpolation, on the contrary, aims at finding function that passes exactly through data points.
Approximation
Interpolation
Regardless of the type, the fitted curve provides a compact mathematical formulation of the relationship in your data. Once the curve function is found, it can be used for everything from data visualization to modeling and forecasting. And important aspect here is the ability of the curve to be reused in third-party applications or computer code. The reusability of the curve ensures that dependent variable values can be evaluated for an arbitrary range of independent variable values.
SplineCloud simplifies the process of finding the best fit and ensures curve reusability. Once constructed in the cloud with the help of the curve fitting tool, your fit curves become accessible over SplineCloud API, so you can retrieve and restore them in your computer code with the help of general libraries for B-splines or NURBS. For more smooth experience SplineCloud also provides open client libraries for Python and MATLAB, which automate curve load and evaluation.
Curve Fitting Methods
Numerous algorithms have been developed over decades to tackle the task of finding the best fit to data. In the conventional approach, the choice of the appropriate method relies on the specific characteristics of the data and the intended application. However, there exist universal methods that are applicable to the majority of cases. Among these, understanding different types of curve fits can help in selecting the optimal approach. But let's first take a look at the most common options.
Linear and Polynomial Curve Fitting
The simplest approaches of linear and polynomial regression are the most popular, regardless of their drawbacks. Linear curve fitting works fine only in two cases:
- Data shows evidence of linear behavior → you can use a simple equation.
- Data is big enough so that the interpolation error is relatively small → you can use piecewise linear fitting.
Linear function
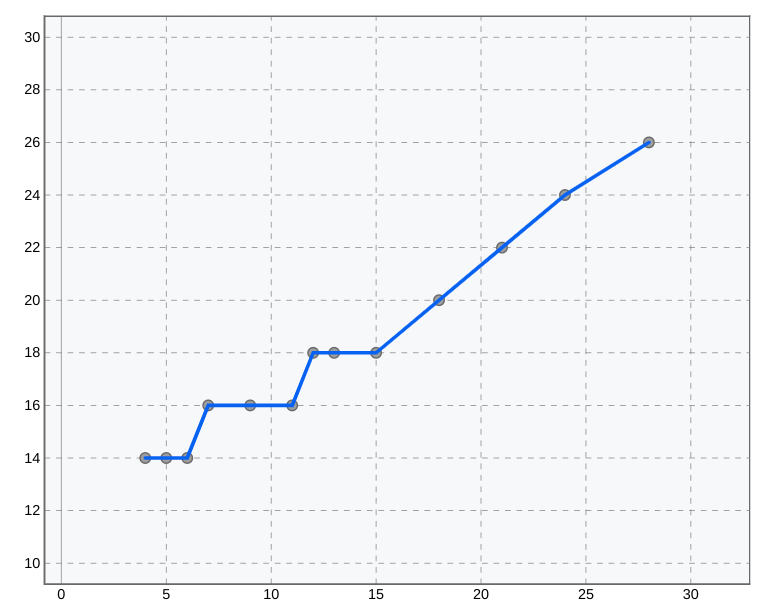
Piecewise linear fit
Some nonlinear relations in data can be fitted with polynomials. Simple polynomial fitting uses curve fitting equations like . Polynomial curve fitting and piecewise polynomial regression work better in cases when data show evidence of nonlinear behavior, and the number of data points is not sufficient to neglect the errors obtained by linear models. However, polynomial fitting often leads to the issue of overfitting, especially for high-order polynomials, causing the curve to oscillate between data points, resulting in a drastic increase of the error.
Cubic polynomial fit
Overfitting
Spline Functions
Obtaining smooth curves is important when data contains measurement noise or natural variability. This is a perfect application for approximation with spline functions, and particularly smoothing splines.
Smoothing Splines
Smoothing splines are a versatile and non-parametric method for curve fitting, designed to balance accuracy and smoothness. They work by representing a curve as a linear combination of smaller, simpler functions called basis splines (B-splines). Each B-spline affects only a specific portion of the data range, making smoothing splines ideal for modeling complex shapes while avoiding excessive oscillations.
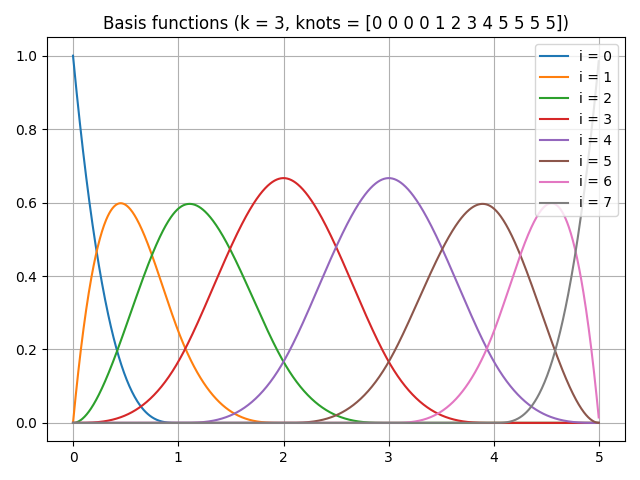
B-Spline basis functions
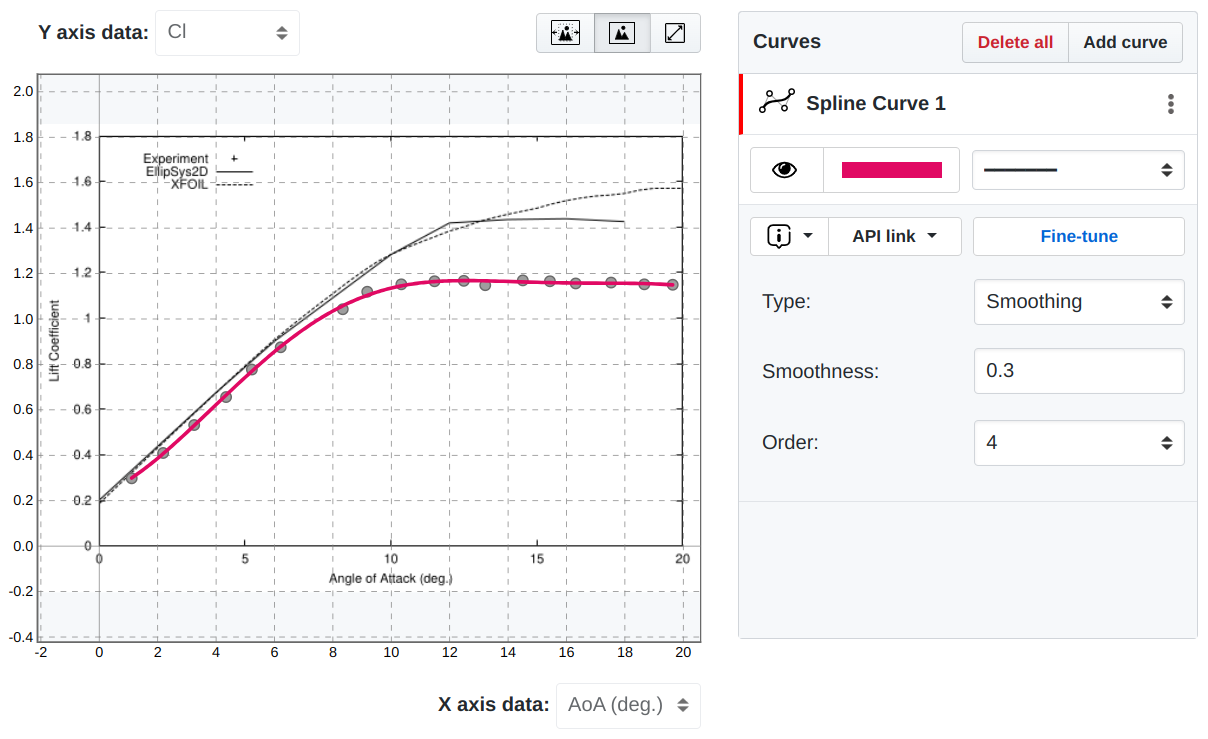
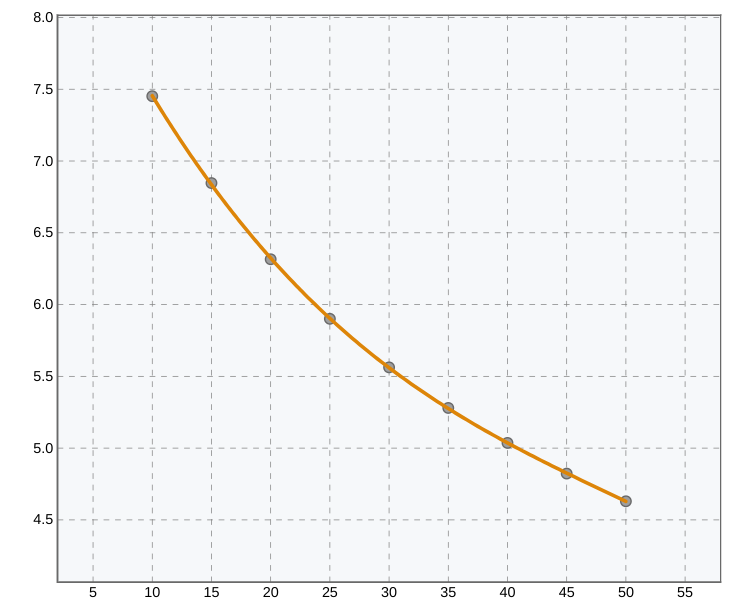
Smoothing spline curve fitting with SplineCloud
The solution for a smoothing spline fit is based on minimizing a cost function that combines a goodness-of-fit term and a penalty term. The penalty term is based on the curvature of the curve, which helps control the level of smoothness (s-factor). The smoothing spline finds the optimal balance between fitting the data closely and keeping the function simple, preventing overfitting.
The smoothing spline algorithm is available in the SciPy library 'interpolate' module. It is also a SplineCloud’s default fitting method. The curve shape can be adjusted via a set of parameters:
- Smoothness factor – controls the number of knots, and eventually the curvature of the spline.
- Degree (order) of the underline B-splines.
- Knot positioning – can be used to tune local curvature in some regions.
Least Squares
This is a different method for finding the optimal spline function to fit a set of data points. It works by minimizing the sum of the squares of the offsets (residuals) of data points from the curve. Still, the target of the curve fitting algorithm is similar and is aimed at finding the balance between smoothness and adhering closely to the data points.
SplineCloud also supports the Least Squares method, so you can choose what works best for your data.
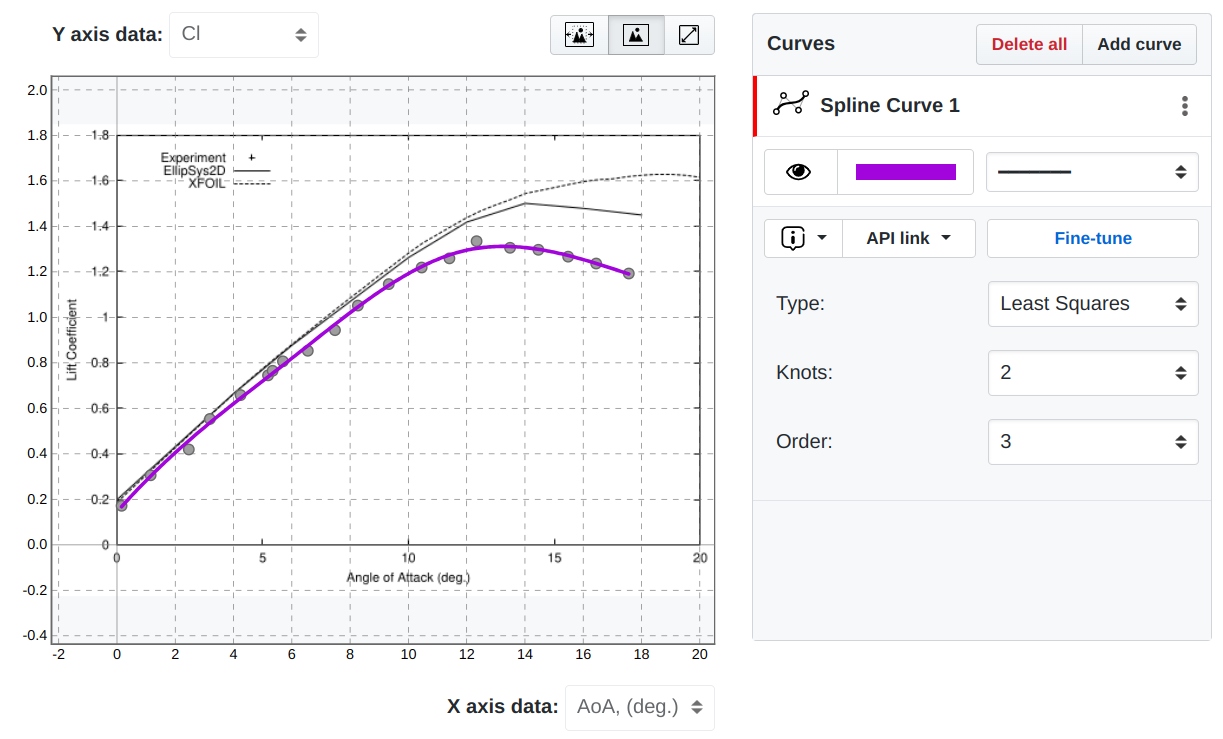
Least squares spline fitting with SplineCloud
Interpolating Splines
Interpolating splines in fact is just an edge case for smoothing splines, for which a smoothing factor equals to 0, meaning no smoothing is applied and a maximum number of knots is selected. Use this method if you need to obtain an exact fit for your data.
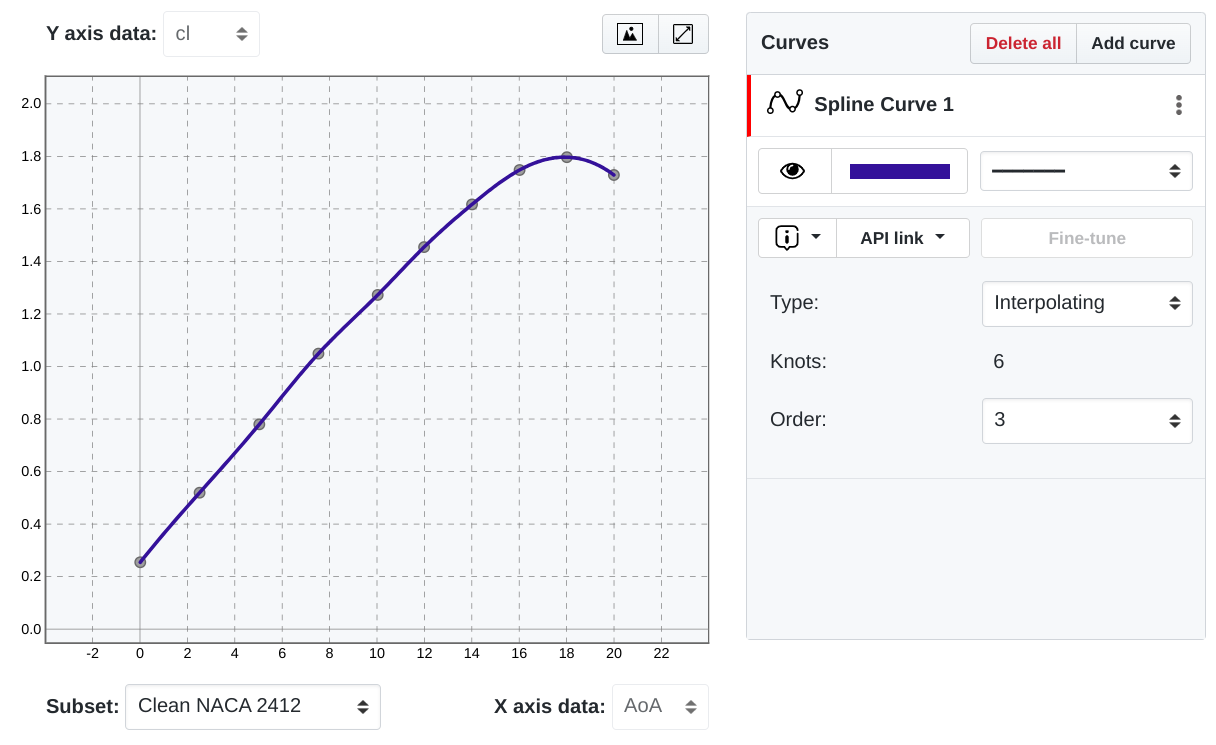
Spline interpolation with SplineCloud
Other Methods
In addition to polynomials and splines, mathematicians have developed numerous specialized curve fitting functions. Understanding different types of curve fitting can aid in selecting the most effective approach for specific scenarios. Methods like Fourier series, Taylor polynomials, Chebyshev polynomials, Rational Thiele interpolation and others excel at fitting certain data types.
Fourier series fit periodic data by superimposing sine waves. Taylor polynomials approximate local behavior via point derivatives. Chebyshev polynomials minimize error through orthogonal bases. Thiele interpolation uses a rational function that is expressed as a continued fraction. These curve fitting techniques, while powerful, shine best only for particular data characteristics and their complexity and narrow focus limit broader applicability.
Splines, on the contrary, stand out for offering a flexible and generalizable approach. They make no assumptions about function form or derivatives. The piecewise nature of splines allow both global and local control, which makes them an excellent default choice before considering more exotic methods. The simplicity and intuitiveness of spline construction and manipulation make them accessible to experts and non-experts alike.
And by selecting spline methods, consider parametric splines, as they put the flexibility of the shape and ease of use to the next level.
Parametric Splines
Although spline functions are highly adjustable and provide control over fit tolerance and curve shape, sometimes it is still not enough. Data may contain important local patterns that are hard to reproduce while preserving global smoothness. And this is where parametric spline fitting shines.
Basically, a parametric spline curve is represented by two distinct spline functions that use the same knot vector. This provides the ability to represent much more complex shapes. Essentially, due to their ultimate flexibility and variety of options for shape control, parametric spline curves and surfaces are widely used in computer graphics systems and professional CAD systems.
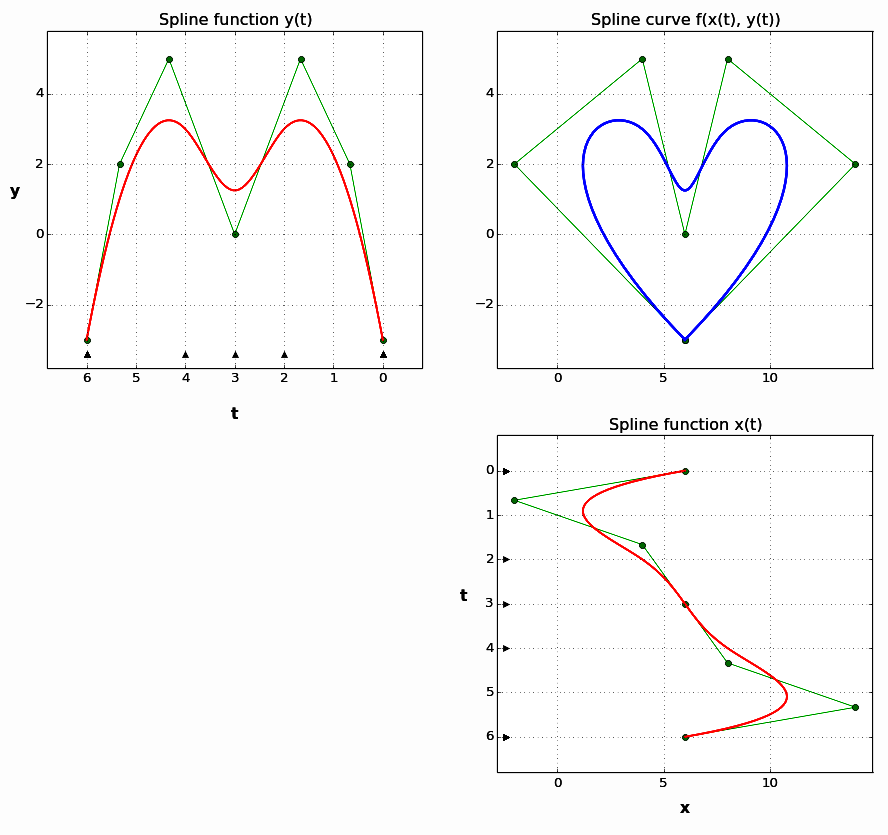
Parametric spline curve represented by two spline functions
In addition to the knot vector and degree, in the case of parametric splines, the shape of the B-splines can be adjusted by changing the position of the corresponding control points and their weights. Dragging control points mimics how designers create curves in CAD software.
Control points clustered closer together result in higher local curvature, while wider spacing creates flatter sections. The weight of each control point determines how strongly it influences the curve shape. Higher weighted points pull the spline closer to its position. Lower weights let the curve pass farther away.
This level of customization is available in SplineCloud through a Fine-Tune Mode. You can add, drag, and remove control points on the screen to tweak the curve shape. Adjusting weights further sculpts the fit locally. The hands-on control takes curve fitting beyond predefined algorithms and unlocks the ability to find the best possible fit for the cases when default fitting algorithms do not satisfy expectations.
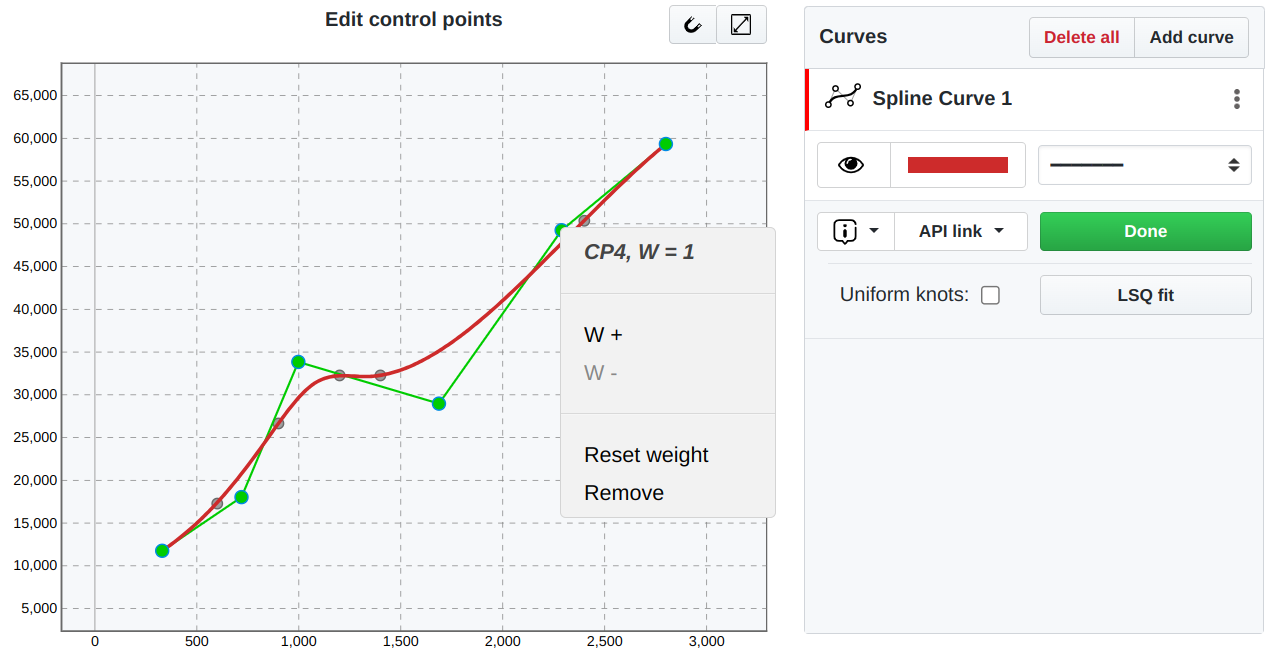
Fine tuning spline curve shape
Moreover, Fine-Tune mode enables interactive adjustment of the knot vector of the spline curve. The knots partition the spline into segments, and altering the knot vector impacts the curvature both locally and globally. Moving knot positions slides where segments of the spline start/end, shifting where it can bend. Adding more knots gives the spline more freedom to bend and fit complex patterns in the data. Each knot enables an additional degree of localization. Removing knots forces the spline to be smoother and less inclined to overfit. With fewer segments, it behaves more like a global polynomial. By adding repeating knots you can adjust the continuity of the spline, introducing sharp corners or even flat areas if needed.

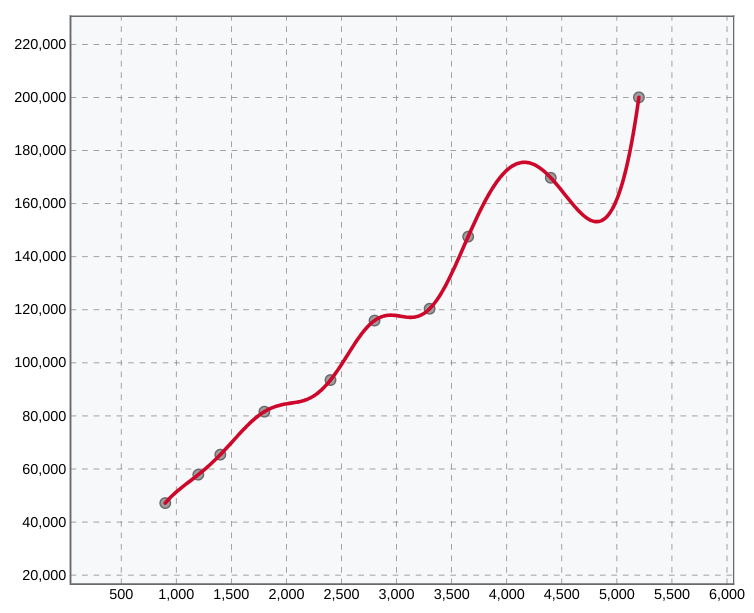
Adjusting knot vector to fit complex nonlinear step function
Eventually, knots and control points of parametric splines serve as virtual “handles” for shaping spline curves interactively. Adjusting their positions grants localized influence over the curve:
- Adding/removing knots controls number of bendable segments
- Dense knots enable tight bending, sparse knots impose smoothness
- Dragging knots slides segment boundaries of the spline
- Repeated knots sharpen inflections at that point
- Control points pull the curve towards their position
- Closer control points induce tighter curvature
- Adjusting weights scales localized influence of points
Together, knots and control points provide an intuitive what-you-see-is-what-you-get editing experience. You see the fitting curve reshape as you drag handles on the screen. This direct manipulation grants flexibility beyond preset algorithms. You can sculpt splines to match nuanced data features that mathematical fits miss.
The interactive feedback builds physical intuition for how splines work. Over a several trials you will quickly develop a feel for tweaking knots and control points to achieve desired curves. With Fine-Tune mode curve fitting transitions from being abstract mathematical approach into tangible user-controlled design method.
Reusing Fit Curves in Code
The ability to reuse curves in external applications is another strong advantage of the SplineCloud approach. Once you achieve the ideal fit interactively, you can export curve parameters and restore it in your code, or use the curve API link to automate access to curve data. The majority of modern systems for computer math and data analysis have packages for working with B-splines and NURBS, so restoring curves in the code should be straightforward.
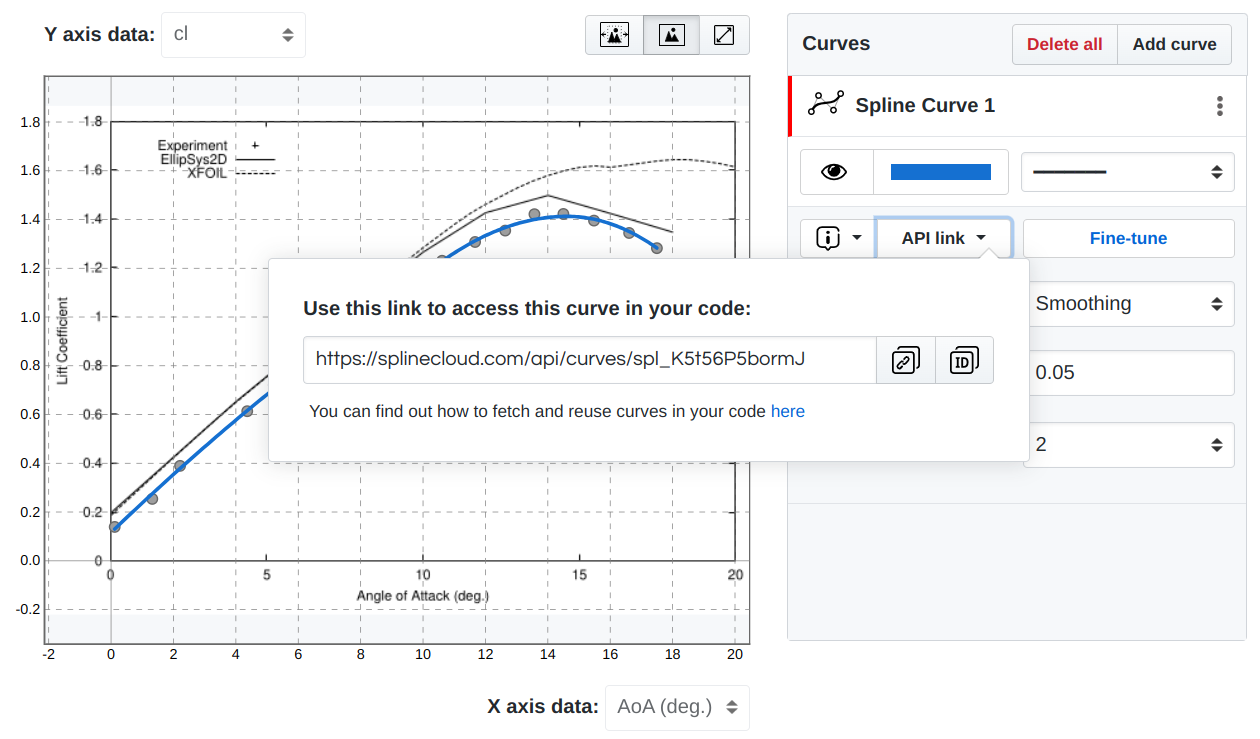
API link to constructed curve
SplineCloud also provides client libraries for both Python and MATLAB that automate curve load and construction in your code. With just a few commands the fitted splines from the cloud transition into a callable function in your code, so you can reuse them to build more complex models on top, perform comparison, numerical analysis, integration, and optimization, or simply generate plots.
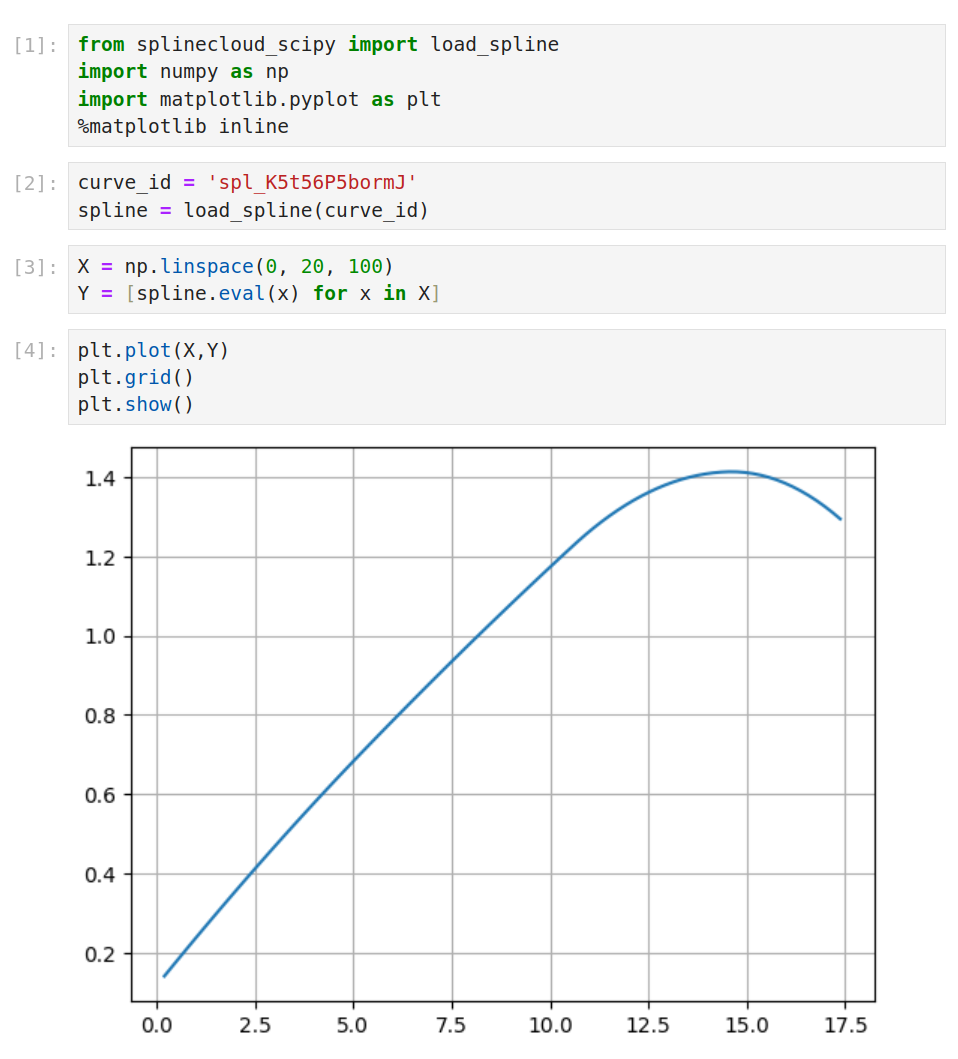
Reuse of Spline Curve in Jupyter Notebook
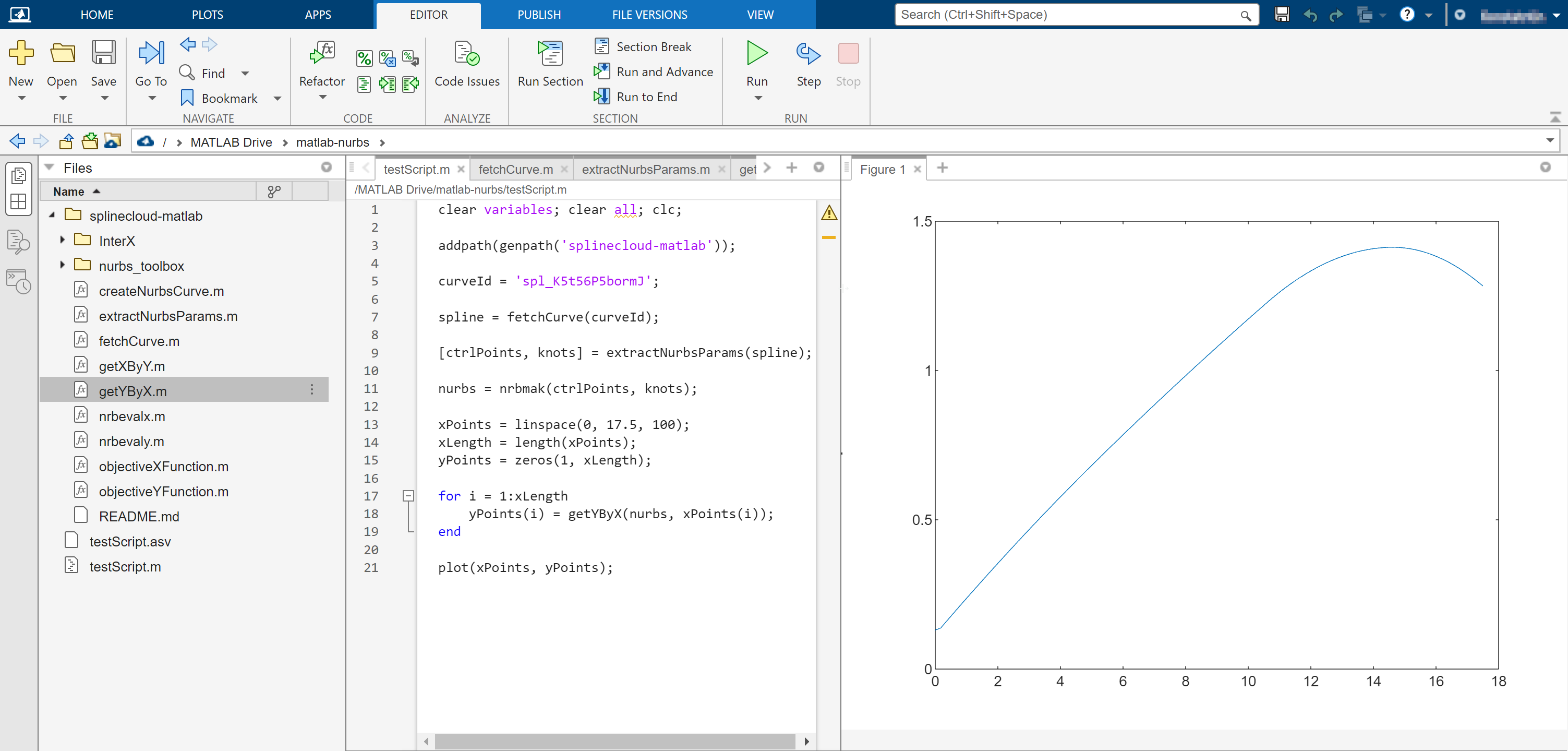
Reuse of spline curve in MATLAB
Treating splines as standard callable functions makes them powerful building blocks in code. And by interactively fitting splines online first, you remove coding busywork, separate data from code, and make it accessible to others.
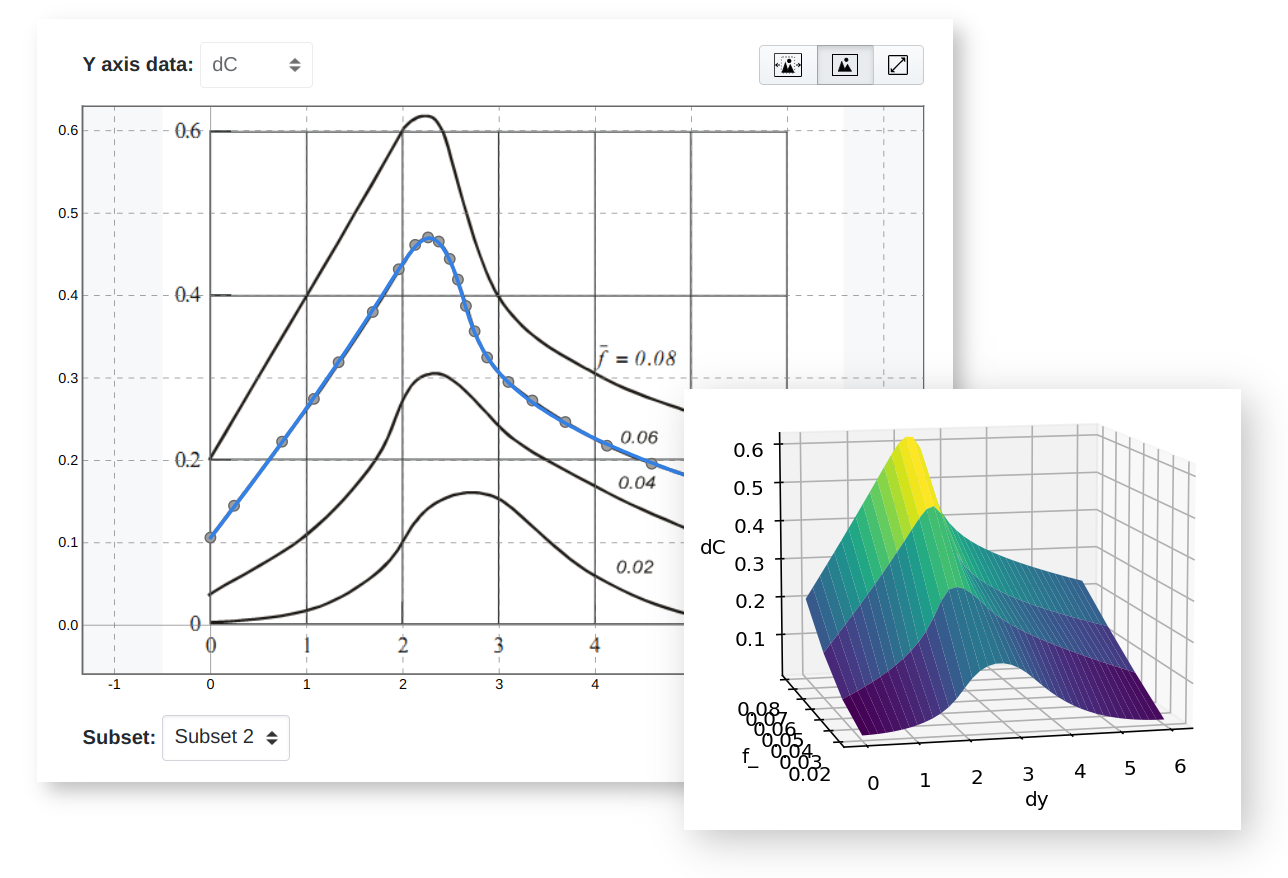
By defining collections of spline curves placed in the cloud it becomes easier to perform deeper analysis and share results with colleagues. Below I provide an example of building a surface plot from four curves loaded from SplineCloud using Python and Matplotlib.
import numpy as np
import splinecloud_scipy as scsp
from scipy.optimize import minimize
import matplotlib.pyplot as plt
curves = {
"f=0.02": scsp.load_spline("spl_P0k4GXa5g701"),
"f=0.04": scsp.load_spline("spl_5rmkerpgIQWL"),
"f=0.06": scsp.load_spline("spl_gCbe99p3reFE"),
"f=0.08": scsp.load_spline("spl_thl4lZnEOZHx")
}
dy_min, dy_max = 0, 6
f_min, f_max = 0.02, 0.08
def surfplot(dy_num=40):
dy_range = np.linspace(dy_min, dy_max, dy_num)
f_range = np.linspace(f_min, f_max, len(surf_data))
dy_vals, f_vals = np.meshgrid(dy_range, f_range)
c_vals = np.array([[curves[f"f={fv}"].eval(dy, extrapolate=True) for dy in dy_range] for fv in f_range])
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(dy_vals, f_vals, c_vals, cmap='viridis')
ax.set_title('dC(dy, f_)')
ax.set_xlabel('dy')
ax.set_ylabel('f_')
ax.set_zlabel('dC')
ax.view_init(elev=15., azim=45.0)
plt.show()
surfplot()
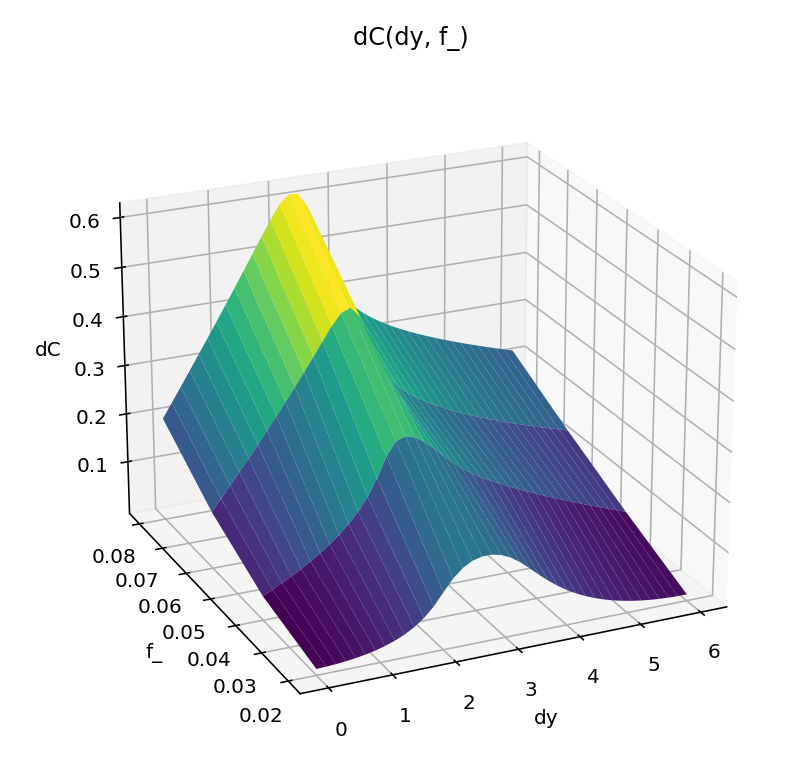
Surface built from spline curves loaded from SplineCloud
Conclusion
Curve fitting is a foundational technique in data analysis, bridging the gap between raw data and actionable insights. By understanding various fitting methods, from traditional polynomials to advanced splines, you can better model relationships in your data, predict trends, and optimize performance. While each method has its strengths and applications, spline functions stand out for their flexibility, smoothness, and ability to adapt to diverse data characteristics. SplineCloud simplifies the curve-fitting process, empowering users with an interactive toolset and robust API integration. Native integration with plot digitizing tool allows to extract curves from graphs, while the Fine-Tune mode enables precise control over spline shapes, making SplineCloud an invaluable resource for engineers, researchers, and analysts. Moreover, the platform's seamless integration with Python and MATLAB ensures that fitted curves are not only accurate but also reusable in code. Whether you're smoothing noisy data, visualizing complex trends, or constructing sophisticated models, SplineCloud provides the tools you need to master curve fitting. By combining intuitive interfaces with powerful algorithms, it turns curve fitting from a challenge into an accessible and efficient process, enabling you to focus on deriving meaningful results from your data rather that learning algorithmic approach behind each method.
References
[1] Michael S. Floater, “Splines and B-Splines”, INF-MAT5340-v2007, University of Oslo.
[2] Carl de Boor, “B(asic)-Spline Basics”, In Fundamental Developments in Computer-Aided Geometric Modeling, pages 27–49. Academic Press, London, UK, 1993.
[3] SciPy documentation on smoothing splines: https://docs.scipy.org/doc/scipy/tutorial/interpolate/smoothing_splines.html