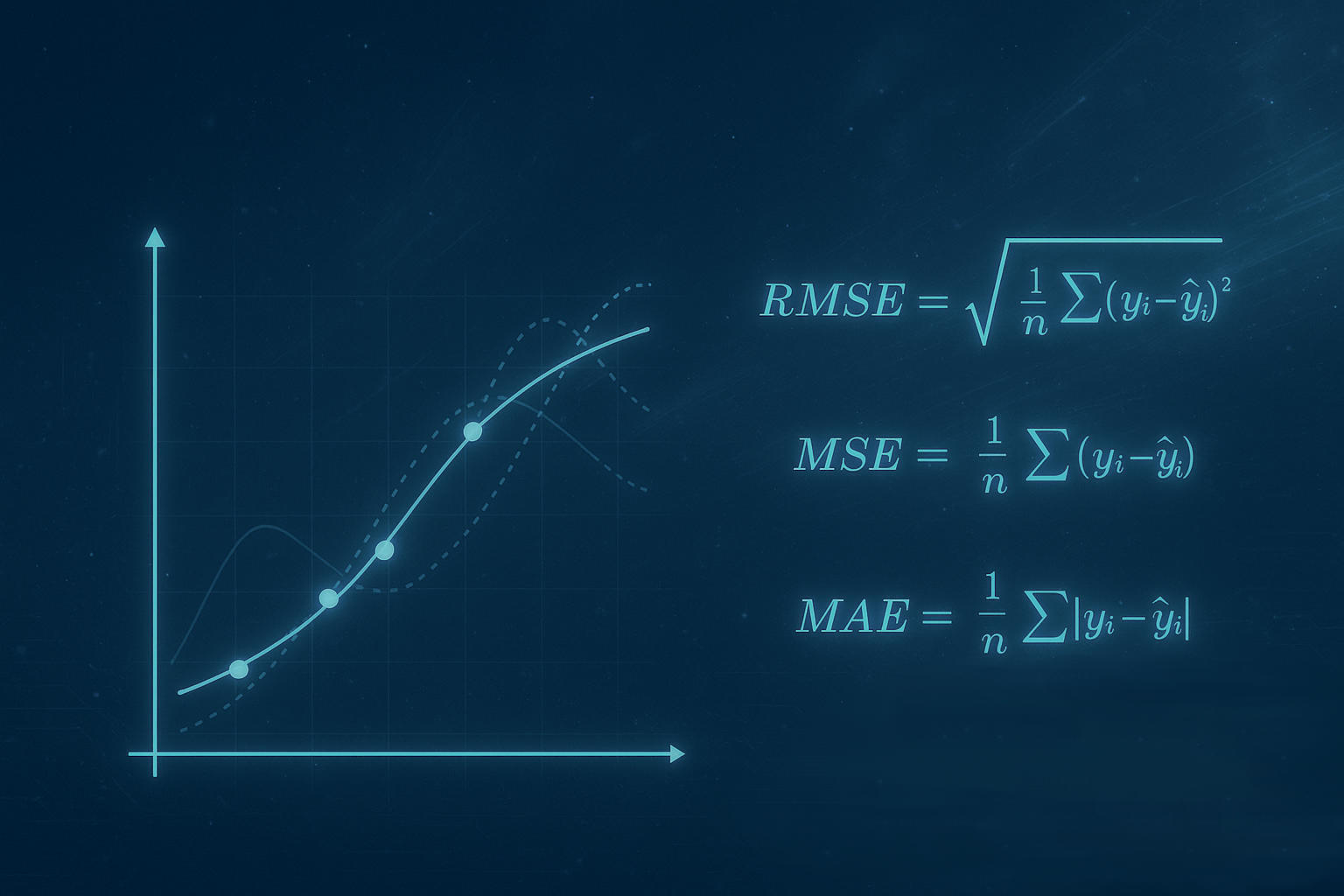
Understanding Curve Fitting Errors: RMSE, MSE, MAE and Accuracy Estimation with SplineCloud

When fitting a curve to experimental or simulated data, it’s not enough to just “draw a smooth line” through the points. The real question is: how well does the model represent the underlying data? To answer this, engineers and scientists rely on error metrics — quantitative measures that compare predicted values against actual observations. These metrics help evaluate the accuracy of the fit, highlight discrepancies, and guide the choice of the most appropriate model. While there are many possible approaches, a few error estimators are used most commonly in practice.

Mean Absolute Error (MAE)

The Mean Absolute Error (MAE) is used to evaluate the accuracy of a fitted model by measuring the average magnitude of the errors between predicted and observed values. It is defined as:

$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - S(x_i) \right|$

where $y_i$ are the actual data values, $S(x_i)$ are the corresponding predicted values from the curve, $n$ is the total number of data points.

MAE provides an intuitive measure of model performance: it tells how far, on average, the predictions are from the actual observations. Unlike squared error estimators, MAE is less sensitive to large individual errors (outliers), making it a useful complementary metric for assessing fit quality, especially when robustness is important.

Mean Squared Error (MSE)

The mean squared error measures the average of the squared differences between observed values $y_i$ and corresponding predicted values $S(x_i)$. It is defined as:

$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - S(x_i))^2$

This metric penalizes larger deviations more heavily, making it sensitive to outliers.

Root Mean Squared Error (RMSE)

The root mean squared error is the square root of the MSE and provides an error measure in the same units as the data:

$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - S(x_i))^2}$

Root Mean Squared Error (RMSE) is one of the most widely used metrics to evaluate curve fitting accuracy. It measures the average magnitude of the errors between predicted and actual values, with larger errors penalized more strongly because the differences are squared before averaging. Finally, the square root is applied to bring the error back to the original scale of the data. Because RMSE is expressed in the same units as the measured data, it’s easy to interpret and compare across different models.

Estimating Fitting Errors in SplineCloud

In SplineCloud, the RMSE is calculated automatically for all curves. The Fit accuracy hint updates after each curve modification (Figure 1). This allows tracking the change of fitting error while applying different fitting parameters, comparing different models and fine-tuned curves against automatically fitted models.

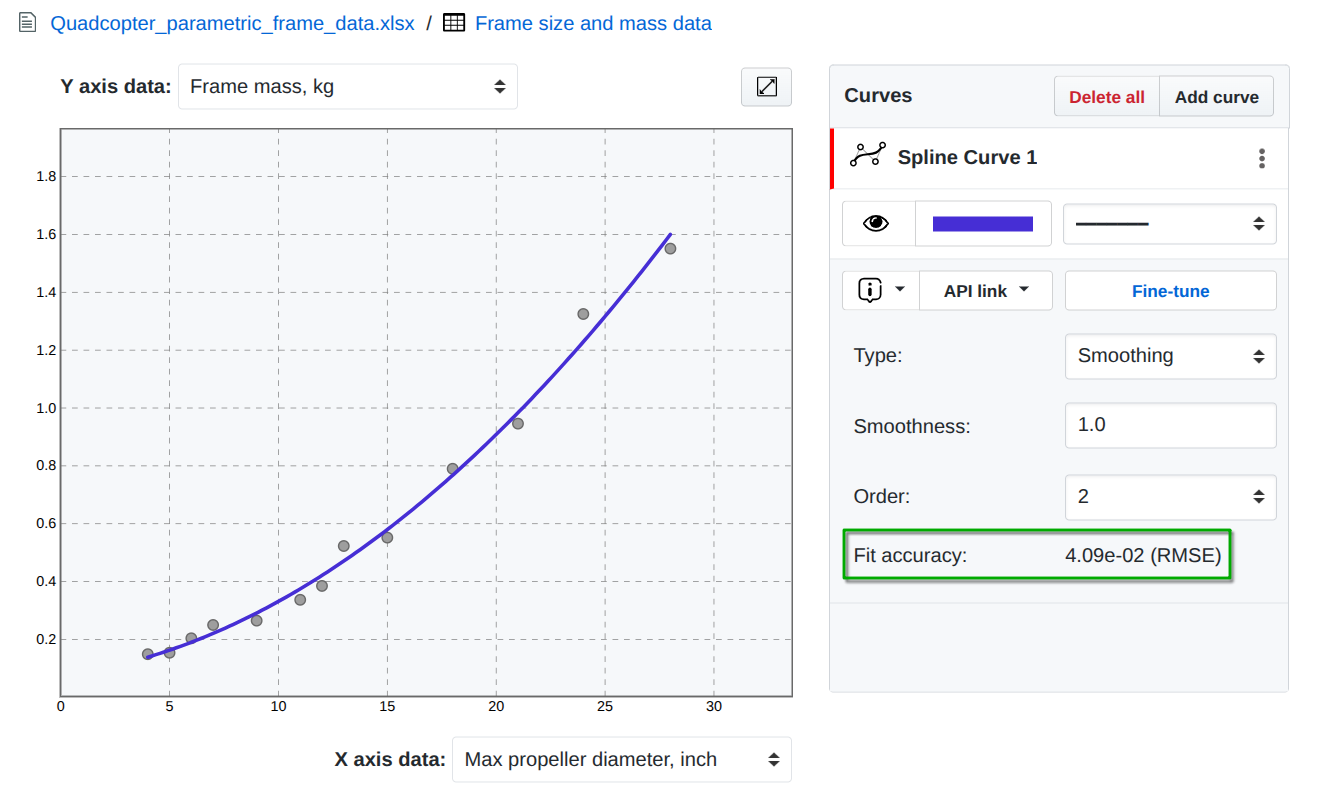
Figure 1. RMSE estimation in SplineCloud

For complex curve shapes, especially those with closed loops (Figure 2), the error between a data point and the curve should not be measured only along the vertical axis. Instead, the true discrepancy is the Euclidean distance from each data point to the nearest point on the curve. This approach is implemented in SplineCloud to estimate fitting errors of parametric curves that approximate data in non-ascending order via RMSE_sd​ - root mean squared shortest distance error:

$\text{RMSE}_{sd} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (w_i d_i)^2 }$

where $d_i$ is the shortest distance between a data point and spline curve and $w_i$ - is the weight of the data point.

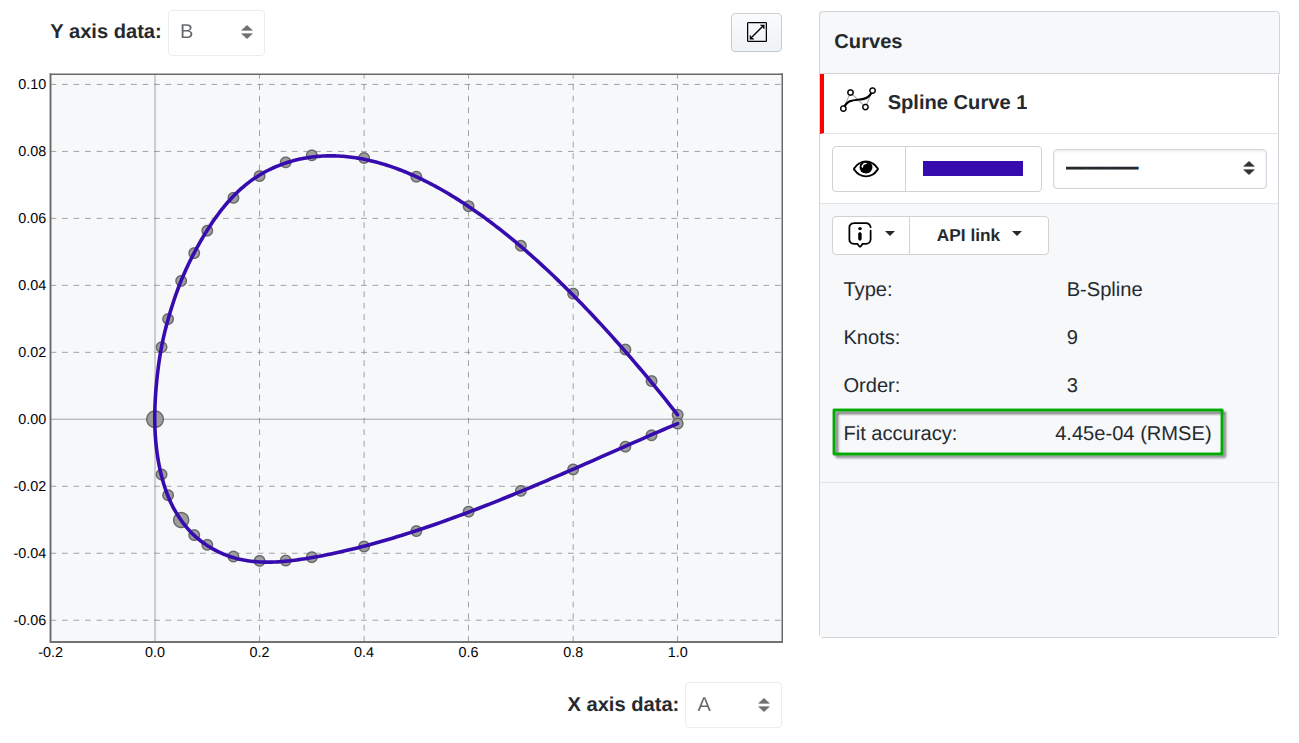
Figure 2. RMSE evaluated via the shortest distance residuals

SplineCloud calculates fitting errors automatically and updates them immediately when curve parameters are modified. This allows you to test different fitting approaches, compare models directly, and observe the impact of each adjustment on the error metrics in real time. The system supports both standard vertical-error measures and shortest-distance estimates for complex parametric curves, providing precise feedback throughout the fitting process.

Conclusions

Evaluating the accuracy of curve fitting is essential for choosing the right model and ensuring reliable results. Metrics such as MAE, MSE, and RMSE provide different perspectives on error estimation: MAE offers robustness to outliers, MSE emphasizes large deviations, and RMSE delivers an interpretable measure in the same units as the data. In SplineCloud, these principles are enhanced with automated error estimation, real-time updates during curve fitting, and advanced distance-based error measures like RMSE_sd for parametric curves. This allows engineers and researchers not only to quantify fitting errors more precisely, but also to interactively compare models and optimize their fitting process with confidence.